Boltzmann relation

In a plasma, the Boltzmann relation describes the number density of an isothermal charged particle fluid when the thermal and the electrostatic forces acting on the fluid have reached equilibrium. Due to their small mass and larger mobility, in many situations the electron density of a plasma is assumed to behaves according to the Boltzmann relation.

If the local electrostatic potential is represented by φ1 and φ2 at two nearby locations, the Boltzmann relation for the electrons takes the form:

ne (φ2) = ne(φ1) exp(-e Δφ/kBTe)

where ne and Te are the electron density and temperature respectively.

A simple derivation of the Boltzmann relation for the electrons can be obtained using the momentum fluid equation of the two fluids model of plasma physics in absence of a magnetic field. When the electrons reach dynamic equilibrium, the inertial and the collisional terms of the momentum equations are zero, and the only terms left in the equation are the pressure and electric terms. For an isothermal fluid, the pressure force takes the form 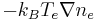-k_BT_e\nabla n_e, while the electric term is 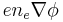e n_e \nabla\phi . Simple integration leads to the expression given above.

In many problems of plasma physics, it is not useful to calculate the electric potential on the basis of the Poisson equation because the electron and ion densities are not known a priori, and if they were, because of quasineutrality the net charge density is the small difference of two large quantities, the electron and ion charge densities. If the ion density is known and the assumptions hold sufficiently well, the electric potential can be calculated simply from the Boltzmann relation.

Discrepancies with the Boltzmann relation can occur, for example, when oscillations occur so fast that the electrons cannot find a new equilibrium (see e.g. plasma oscillations) or when the electrons are prevented from moving by a magnetic field (see e.g. lower hybrid oscillations).

See also

References